추천알고리즘은 크게 사용자가 선호하는 정보를 기반으로 비슷한 아이템을 계산하여 추천하는 콘텐츠 기반 필터링과, 다른 사용자의 과거 행동 등을 통해 얻어진 기호 경향을 활용하여 추천하는 협업 필터링으로 나뉜다. 그 중 협업 필터링은 메모리 기반 방법과 모델 기반 방법으로 다시 한 번 나눌 수 있는데, 모델 기반 방법 중 다양한 행렬 분해 기법이 있다.
정리하자면,
추천 알고리즘 - 콘텐츠 기반 필터링
- 협업 필터링 - 메모리 기반 방법
- 모델 기반 방법 -> 행렬 분해
로 설명할 수 있겠다.
오늘은 이러한 행렬 분해에 대하여 정리해보고자 한다.
추천 시스템에서의 행렬 분해란?
평갓값 행렬을 저차원의 사용자 인자 행렬과 아이템 인자 행렬로 분해하는 것
1. Principal Component Analysis(PCA, 주성분 분석)

PCA는 행렬의 차원을 축소하는 방법이다. PCA의 목적은 데이터를 가장 잘 나타내는 벡터를 구하는 것인데, 이 때 '데이터를 잘 나타낸다'는 말의 의미는 벡터와 데이터 사이의 거리의 합이 최소가 된다는 것을 의미한다. .
데이터의 공분산 행렬을 고윳값 분해(Eigenvalue Decomposition)하여 고유벡터(Eigenvector)를 구하면 데이터의 분산이 최대가 되는 축을 구할 수 있다.(Eigenvector = 벡터의 방향, Eigenvalue = 벡터의 크기)

2. Singular Value Decomposition(SVD, 특잇값 분해)
SVD를 식으로 나타내면 아래와 같이 나타낼 수 있다.

A : m x n rectangular matrix
: ×m orthogonal matrix(AA^T의 eigenvector 제곱근 col vector)
: ×n diagonal matrix(A^TA의 eigenvector 제곱근 col vector)
: ×n orthogonal matrix
식에서 알 수 있듯이 SVD는 행렬을 3개의 행렬로 분해하는 방법이다.
SVD의 가장 큰 특징은 기존의 로 분해되어 있던 A행렬을 특이값(sigma) p개만을 이용해 A'라는 행렬로 ‘부분 복원’ 할 수 있다는 것이다. 특이값이 큰 몇 개만 가지고도 유용한 정보를 유지할 수 있기 때문에 특이값의 크기에 따라 A의 정보량이 결정된다.

Full SVD : 모든 특이값을 이용하는 기법이다.

Thin SVD : 대각원소가 아닌 값들을 이용하지 않는 기법이다. 위에서 설명한대로 수정하자면, 특이값 행렬이 m x n 행렬일 때, m x m 일부 행렬만 이용하는 기법이다.

Compact SVD : 대각원소 중 0인 값들을 제외하고 일부만 이용하는 기법이다. 마찬가지로 수정하자면, m x n 크기의 특이값 행렬에서 특이값들로만 구성된 m x m 행렬 중 0인 값들을 제외하고 r x r 행렬만을 이용하는 것이다. V^T의 크기 역시 수정된 것을 확인할 수 있다.
- 특이값 중 0인 값이 없다면? : Thin SVD = Compact SVD

Truncated SVD : 특이값 중 값이 큰 상위 t개만 이용하는 기법. 특이값 행렬은 t x t 행렬이 되고, V^T도 t x n 행렬이 된다.
특이값을 몇 개 이용하는지에 따라 정보량이 달라지게 되며, 효과적으로 차원이 축소될 수 있다는 장점을 가진다.
https://angeloyeo.github.io/2019/08/01/SVD.html
해당 링크에 SVD를 기하학적으로 표현한 GIF가 게시되어 있다. 해당 자료를 확인하면 더욱 직관적으로 이해할 수 있을 것 같다!
3. Nonnegative Matrix Factorization(NMF, 비음수 행렬 분해)
행렬 분해시 사용자와 아이템 각 벡터의 요소가 0 이상이 되는 제약을 넣는 방법이다.
$$ A\approx W \times H $$
앞에서 봤던 PCA, SVD와의 차별점은 W와 H의 값들이 모두 음수가 아니어야 한다는 것이다!
이를 위해
f= \left\|A−WH \right\|^2_F
먼저 W, H를 음수가 아닌 랜덤 값으로 초기화 한 뒤, f를 최소화하는 방향으로 W와 H를 업데이트한다. f가 최소가 될 때까지 계속 수렴검사와 업데이트를 반복하면 W와 H값을 구할 수 있다.
여기서 정리를 한 번 하고 넘어가자면, 어떤 데이터를 이용하는지(명시적 or 암묵적), 결측값이 있을 때 결측값 처리를 어떻게 하는지(평균/0으로 채우기 or 이용X 등)가 추천 시스템의 다양한 행렬분해에서 중요한 포인트가 되는 기준이다. SVD와 NFM는 모두 명시적인 데이터를 이용하며 결측값은 0 혹은 평균값으로 채운다.
4. Matrix Factorization(MF)
MF는 SVD와 마찬가지로 명시적인 평갓값에 대한 행렬 분해를 하지만 SVD와 달리 결손값을 메꾸지 않고 관측된 평갓값만 사용하여 행렬을 분해하는 방법을 말한다.
MF의 장단점을 정리해보자면, 콘텐츠 기반 협업 필터링이나 SVD보다 성능이 좋고, sparse한 데이터에 강하고, 확장성이 좋다는 장점이 있으나(결측값을 아예 사용X -> 사용자와 아이템이 많아져도 기존 성능 유지 가능) 사용자와 아이템이 많아지게 되면 학습 속도가 느리고 병렬 처리가 불가능하다는 단점이 있다.

Matrix Factorization은 관측된 선호도만 이용하기 때문에 (결측값에 대한 값을 이용하지 않음) 과적합을 피하기 위해 Regularized Squared Error를 사용한다.
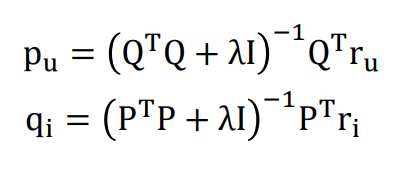
알고리즘을 해결하기 위해 SGD(Stochastic Gradient Descent) 혹은 ALS(Alternating Leatst Squares)를 이용한다. 특히 ALS는 q와 p를 번갈아서 고정하여 최소제곱법을 이용하여 해결하는 방법이다.
식을 풀면 왼쪽과 같이 풀 수 있다.
참고링크
https://blog.naver.com/jinp7/221312142481
https://sirzzang.github.io/etc/etc-svd/
https://ko.wikipedia.org/wiki/%EB%B9%84%EC%9D%8C%EC%88%98_%ED%96%89%EB%A0%AC_%EB%B6%84%ED%95%B4
https://blog.naver.com/PostView.naver?blogId=shino1025&logNo=222394488801
https://velog.io/@vvakki_/Matrix-Factorization-2
'AI' 카테고리의 다른 글
| [논문 리뷰] Neural Feedback Text Clustering with BiLSTM-CNN-Kmeans (3) | 2024.12.05 |
|---|---|
| Video Classification (2) | 2024.11.21 |
| 규제_Lasso, Ridge, Elastic-Net (1) | 2024.09.26 |
| 이미지 데이터 증강 : CutMix (0) | 2024.09.19 |
| [논문 리뷰] Visible and Thermal Camera-based Jaywalking Estimation using a Hierarchical Deep Learning Framework (0) | 2024.09.12 |



